I just went through the material of the first week of Combinatorial Mathematics, which is offered by Tsinghua University through EdX. My initial impression is that this is a mildly engaging course, marred by subpar presentation. Thus, I have a hard time recommending it in its current iteration.

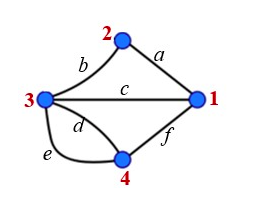
One of the assignments in the first week reminded me of a program I posted some time ago. In Finding an Eulerian Path I present a somewhat verbose program for finding an Eulerian path in a graph of which it is known that it contains an Eulerian path. On the other hand, the assignment in that EdX course asks for the total number of Eulerian paths of this undirected multigraph:

That’s not a particularly challenging question. It was more fun for me to write a neat Haskell program to solve this task. However, instead of just counting all Eulerian paths, my program finds all of them. The code, which is given below, is quite clean and should be easy to follow. Let me describe the algorithm I’ve implemented in plain English, though.

For all nodes in the graph, the program finds all Eulerian paths starting from that node. The relevant part of the program at this step is the function call “findPath’ [(“”, node, g)] []”. When you set out to find all Eulerian paths, the string indicating the current path is empty. As the graph is traversed, that string grows. Two cases are possible. First, we could have reached a dead-end, meaning that there are untraversed edges that can’t be reached from the current node, due to the path that was chosen. Second, if there are reachable nodes left, then the traversal continues by using any of the unused edges.

This can be modelled in a rather intuitive functional style with a list containing elements of the structure “(Path, Node, [Edge])”. Start by taking the head of that list, and figure out whether there are any edges left to take from that position. If so, then discard the head, and append all possible paths to the list. In the given example, starting at node 1, the current path is the empty string, and the list of edges contains the entire graph. Subsequently, three elements are added to the list, with the respective paths “a”, “c” and “f”, and a list of remaining edges of which the edge that was just chosen was removed from. This goes on, recursively, until the entire graph has been processed. Of course, if there are no edges left to traverse, we’ve found an Eulerian path.

With this description, the program below should be straightforward to follow. To run it, with a graph modelled after the image above, load the code into GHCi, and execute it by typing “findPaths graph nodes”.

import Data.List

type Node      = Int
type Edge      = (Char, (Int, Int))
type Graph     = [Edge]
type Path      = String
type Candidate = (Path, Node, [Edge])

graph :: Graph
graph = [('a', (1,2)),
         ('b', (2,3)),
         ('c', (1,3)),
         ('d', (3,4)),
         ('e', (3,4)),
         ('f', (1,4))]

nodes :: [Node]
nodes = [1..4]

findPaths :: Graph -> [Node] -> [Path]
findPaths g ns = findPaths' g ns []

findPaths' :: Graph -> [Node] -> [Path] -> [Path]
findPaths' _ []     acc = acc
findPaths' g (n:ns) acc = findPaths' g ns acc' 
    where acc' = findPath g n ++ acc
  
findPath :: Graph -> Node -> [Path]
findPath g node = findPath' [("", node, g)] []

findPath' :: [Candidate] -> [Path] -> [Path]
findPath' []                    acc = acc
findPath' ((path, _, []):xs)    acc = findPath' xs (path:acc)
findPath' ((path, node, es):xs) acc
    | null nextEdges = findPath' xs acc  -- dead-end, discard!
    | otherwise      = findPath' (xs' ++ xs) acc
    where nextEdges  = filter (\(_,(a, b)) -> a == node || b == node) es
          xs'        = nextPaths (path, node, es) nextEdges []

nextPaths :: Candidate -> [Edge] -> [Candidate] -> [Candidate]
nextPaths _                []     acc = acc
nextPaths (path, node, es) (x:xs) acc = nextPaths (path, node, es) xs acc'
    where acc'  = (path', node', delete x es ) : acc
          path' = path ++ [label]
          node' = if node == a then b else a
          (label, (a, b)) = x