Last week Rice University’s MOOC Principles of Computing started on Coursera. Judging from the first week’s material, it seems to have all the great qualities of their previous course An Introduction to Interactive Programming in Python: The presentation is well done, there is plenty of support available, and the assignments are fun. The very first assignment was writing the game logic of 2048.

I don’t consider 2048 to be particularly interesting due to fundamental flaws in its design. First, it can’t be won from any starting position. Second, the most promising strategy makes it rather tedious, and further exhibits that it’s about having a lucky streak with the random number generator instead of skill. Personally, I prefer games that exhibit what is sometimes referred to as “theoretical perfection”, i.e. the attribute of a game that playing it perfectly makes victory a certainty. While 2048 is, as a consequence, rather unappealing to me, I can see why some people would enjoy sliding tiles around.

Writing the code for the game logic was rather straightforward. Due to Principles of Computing using Python as a teaching language, it was no surprise that the one mistake in my initial solution was due to mutation. Thinking that this would have been much more fun in Haskell, I then proceeded to write a complete implementation of 2048 in that language, including I/O handling. The entire source code is available on my Github account. As it turned out, the more complete Haskell solution required fewer lines of code than merely the game logic in Python.

As a side note, if you came to this page because you were looking for a solution to the Python assignment of Principles of Computing, you’re wasting your time. The Haskell implementation is fundamentally different from an implementation in Python, and uses programming language constructs that are not even available in that language. In other words, looking at the Haskell source code will not help you if you are struggling with this assignment.

In this article I only want to highlight the core part of the game logic, since it nicely demonstrates the power of functional programming. First, I defined a datatype for the direction the numbers in the grid can be moved in, and a type synonym for a list of lists of integers, to increase the readability of type signatures. This should be evident from the signature of the function ‘move’ further down, which takes as an input a grid of numbers and a move, and produces a new grid.

data Move = Up | Down | Left | Right
type Grid = [[Int]]   

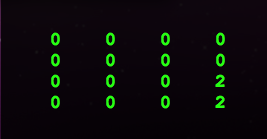
The game 2048 is played on a 4 x 4 board. The starting position in my implementation is fixed:

start :: Grid
start = [[0, 0, 0, 0],
         [0, 0, 0, 0],
         [0, 0, 0, 2],
         [0, 0, 0, 2]]

The board can be moved in four directions, meaning that all numbers move in that particular direction, and if two numbers, when moved in the same direction, end up next to each other, they merge. For instance, in the starting position shown below, moving the board in the direction ‘Up’ turns the board into:

[[0, 0, 0, 4],
 [0, 0, 0, 0],
 [0, 0, 0, 0],
 [0, 0, 0, 0]]

If the grid in the starting position was moved ‘Right’, there would be no change. If the grid changes, then a new number spawns on any empty tile, and this number can be either 2 or 4.

Looking at this mechanic, the question is how it could be modelled effectively. Any row or column on the grid can be understood as a list. The relation between rows and lists is straightforward. The columns will have to be extracted, modified, and inserted again, though. Or maybe they don’t?

I wrote a function to merge a row or a column, represented as a list. First, all zeros are removed. Then, the list is processed, merging adjacent elements if they contain identical numbers, and padding the result of that operation with zeroes, if necessary.

merge :: [Int] -> [Int]
merge xs = merged ++ padding
    where padding          = replicate (length xs - length merged) 0
          merged           = combine $ filter (/= 0) xs
          combine (x:y:xs) | x == y    = x * 2 : combine xs
                           | otherwise = x     : combine (y:xs) 
          combine x        = x

The merge function can be directly applied when the board is moved to the left. The other directions require a little bit of thought, if the code is supposed to remain clean. Moving the grid to the right is done by taking each row, reversing it before handing it off to the function ‘merge’, and then reversing the result again:

                    
move :: Grid -> Move -> Grid
move grid Left  = map merge grid
move grid Right = map (reverse . merge . reverse) grid
move grid Up    = transpose $ move (transpose grid) Left
move grid Down  = transpose $ move (transpose grid) Right

Moving the grid up or down would be painful if you wanted to extract a column, apply the merge function to it, and then create a new grid with that column inserted. Instead, though, a tiny bit of linear algebra knowledge leads to a much more elegant solution. If it’s not immediately clear how transposing leads to the desired outcome, the please have a look at the following illustration.

        input       transpose   move        transpose

Up:     0 0         0 2         2 0         2 2
        2 2         0 2         2 0         0 0


Down:   2 2         2 0         0 2         0 0 
        0 0         2 0         0 2         2 2

My Haskell implementation uses the terminal as output. It’s not as impressive as the JavaScript frontend of Gabriele Cirulli’s version, but it’s serviceable, as the following two screenshots show:

Overall, I’m quite satisfied with this prototype. There are of course several possible improvements. A score tracker would be trivial to add, while a GUI would be a more time-consuming endeavor. I would find it interesting to have the program immediately react to keyboard input. Currently, every input via WASD requires hitting the enter key for confirmation. Gameplay would speed up a lot if merely pressing a key would trigger the next step in the program execution. I didn’t find any quick solution when researching this problem. The Haskell library NCurses contains constructors for keyboard events, though. I might look into it in case I get an itch to program an “indie” game with ASCII graphics.

If you found this article interesting, then feel free to have a look at the source code of my Haskell implementation of 2048.